Intro to Crypto 1 - CSCG

Category: Crypto
Difficulty: Baby
Author: black-simon

Reconnaissance

Files for you to hack along: intro-crypto1.zip

In the description we have a step-by-step guide (original link) (missing some steps) to solve this.

We have a public key and a message.

By reading the guide we know that we have to try to factor the public key.

Exploitation

At first we have to get the modulus we try to factorize.

To get the modulus, you type:

openssl rsa -pubin -in pubkey.pem -text -noout

pubkey.pem being the public key.

You'll get something like this:

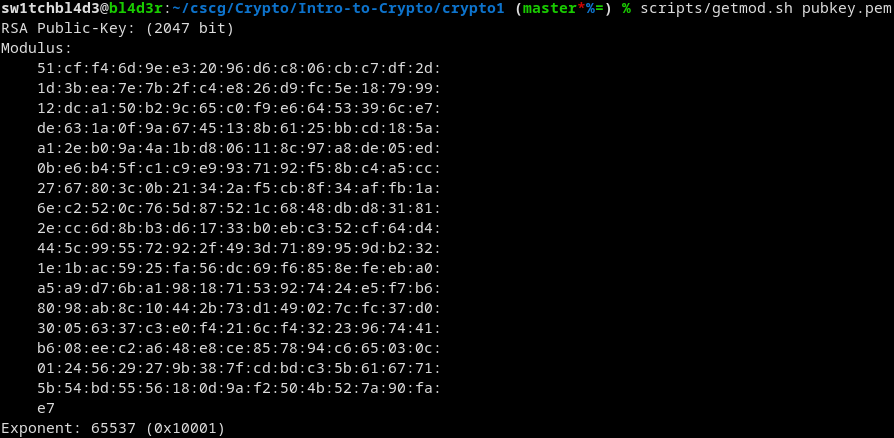
(I put the command into a script in scripts/getmod.sh)

Thats not quite the number we need, this is hex and we need a decimal.

I've done that with this small python script:

from sys import argv
mod = open(argv[1], "r")
modin = mod.read()
mod.close()
modin = modin.replace("\n", "").replace(" ", "").replace(":", "")
print(int(modin, 16))
    

Which basically takes a file as a first argument, reads it, removes newlines spaces and colons and converts it.

You cant really see it because the number is huge (like its supposed to be.)

After that we write a small python script to factor the thing:

N = <put n here>

for i in range(2, 1000000):
    if N % i == 0:
        break
print("p:", i)
print("q:", N//i)
        

This checks if N mod i == 0 (is N divisible by i), and does that for every number from 2 to 1000000.

If that succeeds we have the first prime (and effectively the second one too. (q))

Executing that yields us this:

(thats not the whole q)

Knowing q and p broke the RSA and we can crack it now.

To do that I stole a few functions from Stack Overflow and made this:

p = <insert p>;
q = <insert q>;
e = 65537 # exponent, seen in the getmod.sh
phi = (p-1)*(q-1)

#Took from SO
def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    g, y, x = egcd(b%a,a)
    return (g, x - (b//a) * y, y)

def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        raise Exception('No modular inverse')
    return x%m

print(modinv(e, phi))
    

This script calculates d, the number we need to decrypt the message. (d = e⁻¹ mod ϕ) ( this website helped a lot with formulas etc....)

Execute that and you'll get d.

Once again not the whole d.

Knowing d will let us decrypt the message as shown in the guide:

And we get this!

Mitigation

Have both primes be large, not just one, the encryption is as strong as the weakest prime!

~sw1tchbl4d3, 08/04/2020 (dd/mm/yyyy)